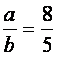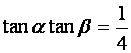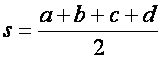|
|
|||
|
|
This is the end of all challenge as Mr. Yue will concentrate on sharing of mathematics in Teaching and Learning webpage this year (2008 - 09). Trigonometry Fun
Solution : Please Click Here |
||
|
|
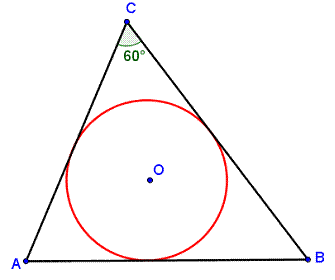
1. In DABC,
ÐC = 60o and If the area of the inscribed circle of DABC
is |
|
|
|
|
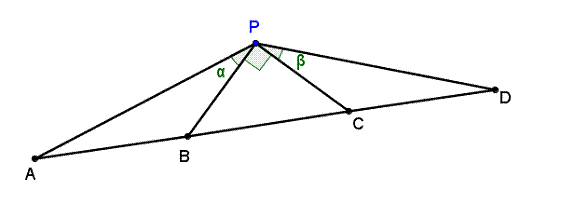
2. In the figure above, ABCD is a
straight line. If AB = BC = CD and ÐBPC is a right
angle, prove
that
|
||
|
|
3. Let D be the area of DABC . It
is given that: Show
that DABC is right-angled. |
||
|
|
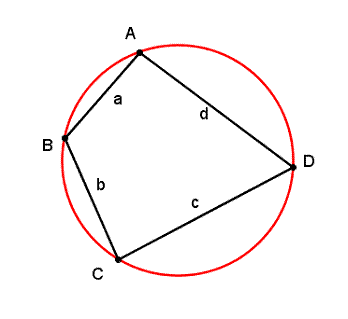
4. Brahmagupta's Formula Brahmagupta (598–668) was an Indian mathematician and
astronomer who discovered a neat formula for the area of a cyclic
quadrilateral. Can you prove this? If D is the area of a quadrilateral inscribed
in a circle, prove that
where |
|
|
|
|
5. Troublesome plane ABCD is a rectangular cardboard with
sides a = 4 and b = 3 . If point A
touches the horizontal ground,
point B is 1 unit and point C
is 2 units above the
horizontal, what is the angle
between the cardboard and the horizontal ? |
|
|
|
|
If you can solve any one or more question, you may
send your solutions to me in WORD file by clicking here. Don’t forget to write
down your name and class (and your school if you are not student of Queen’s
College). Deadline is 9 June
2008. Solutions will be posted
later. There is no material prize.
(The spiritual prize is the joy of learning mathematics.) |
||