Proofs of Cosine Laws

 

First Cosine Law

 

       The first cosine law is also known as the Projection Law as it involves the technique of projecting two sides of a triangle onto the third side.

 

In the diagrams above, DABC has sides  a = BC, b = CA, c = AB.

In Diagram 1, construct AM perpendicular to BC.

 

Then  MC = b cos C, MB = c cos B.

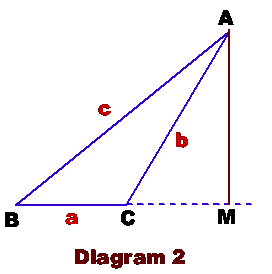
\  a = MC + MB = b cos C + c cos B,    which is the First Cosine Law.

 

In Diagram 2, DABC has an obtuse angle C (= Ð ACB).

Construct AM perpendicular to BC produced.

CM = b cos ACM = b cos (180°-C) = - b cos C

BM = c cos B

\        a = BM – CM = c cos B – (-b cos C) =  b cos C + c cos B

 

Similar result can be obtained if ÐB is obtuse.

 

 

Second Cosine Law

 

       The First Cosine Law has limited applications since it has 5 variables – a, b, c, B, C. We need to know any 4 of them before we can get the fifth. The Second Cosine Law has wider applications since it has only 4 variables. Hence it simply refers as Cosine Law by mathematicians.

 

Rewriting the First Cosine Law cyclically, we get:

            a = b cos C + c cos B                                     (1)

            b = c cos A + a cos C                                     (2)

            c = a cos B + b cos A                                     (3)

 

      (1) ´ a,        a2 = ab cos C + ca cos B             (4)

      (2) ´ b,        b2 = bc cos A + ab cos C                   (5)

      (3) ´ c,              c2 = ca cos B + ab cos A             (6)

 

      (4) + (5) – (6),         a2 + b2 – c2 = 2ab cos C

 

\  c2 = a2 + b2 – 2ab cos C,    which is the (Second) Cosine Law.

 

 

A short proof by Pythagoras Theorem

 

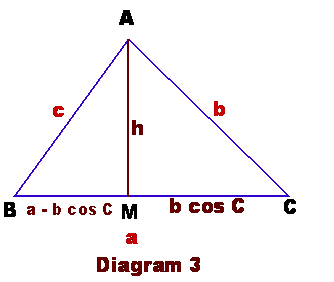
In Diagram 3, let AM = h

Then MC = b cos C

BM = BC – MC = a – b cos C.

Also, h = b sin C.

Applying Pythagoras Theorem in DABM,  we get:

 

c2    = (b sin C)2 + (a – b cos C)2

       = b2 sin2 C + a2 – 2ab cos C + b2cos C

       = a2 + b2 (sin2 C + cos2 C) – 2ab cos C

       = a2 + b2 – 2ab cos C

 

       You may investigate the cases in which ÐB or ÐC is obtuse.

 

 

 

 

 

Geometry Proof

 

       This is the outline of a geometric proof.

From the sides of the triangle, draw 3 squares.

               Area of BCHG      = a2, 

               Area of CIJA         = b2,

               Area of ABFE        = c2.

Draw AM ^ GH,  BN ^ IJ,  CL ^ EF.

It is not difficult to prove that:

       DFBC º DABG   (SAS)

 

Area of FBQL

= 1/2 ´ DFBC  (FB//LC, same base & height)

= 1/2 ´ DABG

= Area of BGMP  (BG//AM)

 

In right- Р DAPC, 

       PC = AC cos C = b cos C

\        Area of CHMP = CH ´ MP = ab cos C.

 

Lastly,

       c2    = Area of ABFE

               = b2 + c2 – 2 ´ Area of CHMP

               = b2 + c2 – 2 ab cos C

              

 

 

 

 

 

The rectangles of the same colour are of the same area!

      Total blue area = 2ab cos C

      Total yellow area = 2bc cos A

      Total red area = 2ca cos B
 
Co-ordinate Geometry Proof

 

  

 

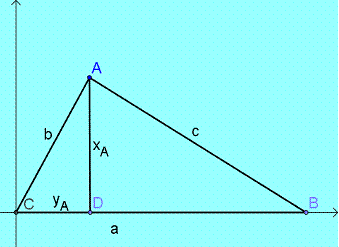
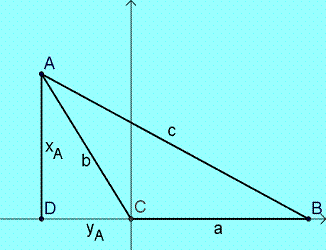
The left figure shows an acute angle C and the right shows the obtuse angle C.

It can be seen that in both cases:

        , 

      B = (a, 0)

      C = (0, 0)

      Using the distance formula for the length  AB,

           

       Now , we expand and simply:

              

                 

                 

                      

 

 

Final Exercise

 

       Prove the First Cosine Law from the Second Cosine Law.