Solve (1 - 2x)(x + 1)(x - 2)(x - 4)(3x - 1) > 0 in one minute !

Step 1 ( 5 seconds)

Rearrange the inequality so that all factors are of the form :

Ax ± B, with A > 0.

Since the first factor in the given inequality (1- 2x ) = - (2x - 1),

the sign of the inequality is changed as in the following :

Result : (2x - 1)(x + 1)(x - 2)(x - 4)(3x - 1) < 0

Step 2 ( 5 seconds)

Find the roots of the equation : (2x - 1)(x + 1)(x - 2)(x - 4)(3x - 1) = 0

Result : x = , -1, 2, 4,

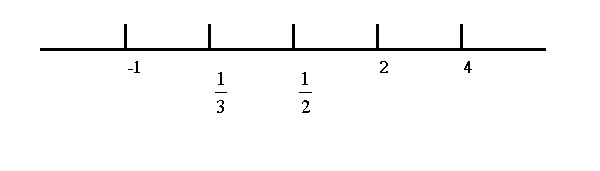
Step 3 ( 10 seconds)

Rearrange the roots in ascending order, and put it on a number line.

The number line needs not in scale.

Result :

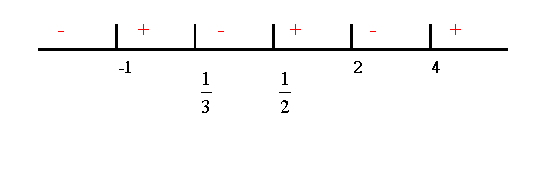
Step 4 ( 5 seconds)

Mark the regions with (+) and (-) signs alternatively,

starting with (+) sign from the far right.

Result :

Step 5 ( 5 seconds)

Find out the regions which satisfy the inequality in Step 1.

(not the original inequality if there is a change in Step 1)

Note that the inequality : (2x - 1)(x + 1)(x - 2)(x - 4)(3x - 1) < 0

is less than zero, the solution of the inequality is the (-) regions in Step 4.

Result :

Solution of inequality : x < -1 or or 2 < x < 4.

Wow! You still have about half a minute to check your answer!

Exercise

(1) Ooooh! Wait a minute. Why this method works? You can use "table method" to do the same question again and compare the procedures. Would you like make a try?

(2) This method can be used to solve inequalities with division, for example:

Care must be taken not to make the denominator zero, that is, x ≠ 2.

Have fun! Try this question.

(3) Solve the inequalities using this method:

(a) (x + 1)(x - 3) > 0

(b) (x - 1)(3 - x)(x + 4)(-2x + 3) ≤ 0

Solution :

(2) x ≤ -1 or or 2 < x ≤ 4

(3) (a) x < -1 or x > 3

(b) -4 ≤ x ≤ 1 or 3/2 ≤ x ≤ 3